Stanford Synchrotron Radiation Lightsource

Fig. 1. Fermi surface and superconducting gap. (a) Fermi surface with node and antinode marked. (b) T=10K gap in Bi-2212 underdoped sample with Tc=92K. v_Δ is the slope of near-nodal portion.

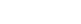
The mechanism of superconductivity in the cuprate high temperature superconductors remains unresolved. One approach to this problem is to understand the phases that exist adjacent to superconductivity on the temperature-doping phase diagram. The pseudogap phase above T_c has been a particular stumbling block because it is not a Fermi liquid as with conventional superconductors. Recently there has been increasing evidence that the pseudogap is a distinct phase from superconductivity that persists below T_c, rather than a precursor to superconductivity. Important contributions to this discovery came from angle-resolved photoemission spectroscopy (ARPES), which observed distinct phenomenology of gaps on different portions of the Fermi surface, implying a picture where superconductivity dominates near the node (along the bond diagonal) and the pseudogap dominates near the antinode (near (π,0)).

Fig. 2. Doping dependence of T=10K energy scales. Momentum-dependence of near-nodal gap fit to the form Δ(k)=v_Δ*0.5*|cos(k_x)-cos(k_y)| (p>0.076) or Δ(k)=Δnode+v_A*0.5*|cos(k_x)-cos(k_y)|. Arrows mark phase boundaries. Data taken at SSRL Beam Line 5-4 (synch) and laser-ARPES lab at Stanford.

In a study recently published in PNAS, researchers at SSRL Beam Line 5-4 and Stanford explored the full doping, temperature, and momentum dependence of spectral gaps in the superconducting state of Bi₂Sr₂CaCu₂O_8+δ (Bi-2212) with unprecedented precision and completeness. What emerges is a clear picture of how the gap in the superconducting state sensitively reflects phases which coexist with superconductivity. This study had three components: low-temperature measurements that revealed three distinct ground states at different dopings; temperature-dependence measurements that revealed that superconductivity suppresses the pseudogap in a momentum-dependent manner; and a revised phase diagram motivated by these data that resolved important discrepancies in the literature.

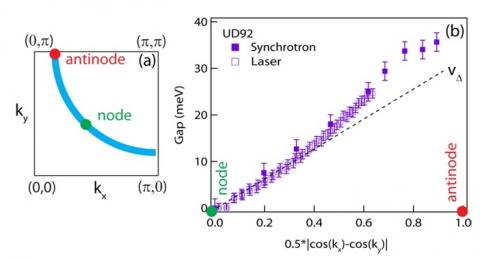
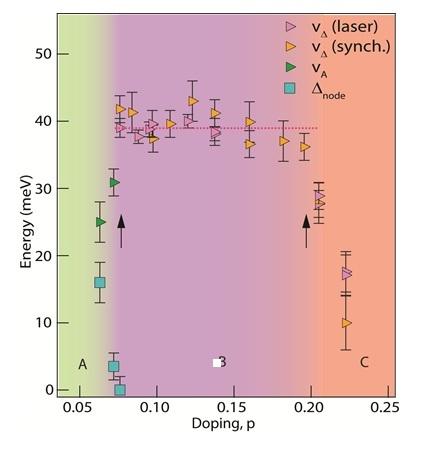
In the superconducting state, the cuprate gap function (Δ(k)) follows a simple d-wave form near the node as a function of momentum: Δ(k)=v_Δ*0.5*|cos(k_x)-cos(k_y)|. In a simple scenario, the prefactor v_D measures the superconducting order parameter. The researchers found three distinct doping regimes where v_D displays different doping dependencies. For p>0.19, v_Δ decreases as T_c decreases; for 0.076<p<0.19, v_Δ is perfectly independent of doping and T_c; and for p<0.076, a fully-gapped phase emerges where the near-nodal gap function has the form Δ(k)=D_node + v_A*0.5*|cos(k_x)-cos(k_y)|. These results are interpreted as follows: the proportional relation between T_c and v_D p>0.19 implies a pure superconducting ground state in that doping regime, and the highly anomalous doping-independent vΔ found at 0.076<p<0.19 is identified as the doping regime where pseudogap and superconductivity coexist when T<<T_c, with support from independent spectroscopic measurements. Thus, p=0.19 is identified as the T=0 endpoint of the pseudogap phase. The phase existing p<0.076 is interpreted as a coexistence regime between superconductivity and another phase distinct from the pseudogap, possibly fluctuating spin-density wave order. Finally, Δ_node does not appear to have a superconducting origin because it persists above T_c.

Fig. 3. Phase competition and revised phase diagram. (a)-(c) Size of momentum region exhibiting pseudogap-like doping dependence (blue shading) decreases below Tc. (d)-(e) size of momentum region exhibiting superconductor-like temperature dependence (pink shading) increases with doping. (f) Phase diagram implied from study, featuring a trisected superconducting dome and pseudogap re-entrance inside the superconducting dome implied by observed phase competition.

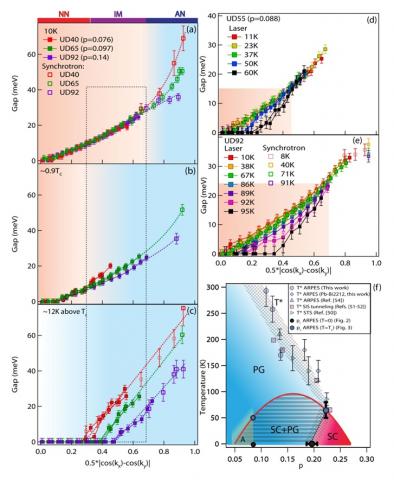
In the temperature-dependence portion of the study, researchers focused on the doping regime 0.076<p<0.19 and inferred the origin of gaps at every momentum based on their phenomenology. The pseudogap phase boundary, T*, increases with underdoping, so a momentum region where gaps followed this same doping dependence was identified with the pseudogap. Likewise, a superconducting gap closes at T_c, so momenta where gaps diminished approaching T_c were identified with superconductivity. It was found that the pseudogap is confined to the antinodal region at low temperature, but at temperatures just below T_c, pseudogap-like doping-dependence is observed over a much larger region of the Fermi surface. This indicates that superconductivity suppresses the pseudogap in a momentum-dependent fashion below T_c, pushing it out of a portion of the Fermi surface. Furthermore, it was found that superconductivity dominates a larger portion of the Fermi surface at higher dopings. This implies that at a sufficiently large doping, the pseudogap exists just below T_c, but is suppressed completely by superconductivity at low temperature.

The low-temperature portion of the study revealed the T=0 endpoint of the pseudogap to be at p=0.19, but surprisingly, when measurements were performed above T_c, the pseudogap was still seen at that doping and slightly higher. This discrepancy is not new, as the endpoint of the pseudogap has been debated in the literature for some time. However, the present research reports it within a single technique, ARPES, and offers a solution with a re-entrant psedudogap phase boundary inside the superconducting dome. This phase boundary is anchored at T=0 and T=T_c by ARPES measurements, and it is naturally implied from the phase competition observed between the pseudogap and superconductivity.