Stanford Synchrotron Radiation Lightsource

A new magnetic state called a quantum spin liquid has been observed by a large international team of investigators from ten institutions¹, including a group using SSRL. When magnetic ions are located within a crystal lattice there are usually strong local magnetic and electric forces between them. At low temperatures such forces lead to a preferred alignment of the atomic moments – in ferromagnets such as iron for example, the atomic magnets are aligned parallel to each other while in anti-ferromagnets they are antiparallel. In other cases the atomic magnetics are aligned along crystallographic axis within the crystal. So quite generally when cooled sufficiently, the atomic moments develop a definite alignment.

Surprisingly that is not the case for Ba₃CuSb₂O₉; for this system there is no preferred orientation of the Cu atomic moments down to 100 mK and the orientations of the atomic magnets are continually fluctuating – as in the continuous motions of atoms in a liquid. Such a system is called a quantum spin-liquid – the atomic magnetic moments are determined by the spin quantum number and the interactions are quantum mechanical in nature. The fluctuation of the magnetic orientations is attributed to so-called frustration - when interactions with different neighbors are in conflict and the orientational alignments arising from these interactions cannot be simultaneously satisfied. Spin liquids have been a hot topic in magnetism for a decade and Ba₃CuSb₂O₉ seems to represent a unique new case.

The magnetic properties were probed using electron spin resonance (ESR) in single crystals. These measurements show that the g-value is isotropic at all temperatures in stoichiometric materials. Magnetic neutron scattering also shows that the spins remain in a quantum fluctuating state to the lowest temperatures, while diffraction studies find that the average structure on mesoscopic length scales is hexagonal – a high symmetry lattice.

These results are surprising however, because the magnetic Cu⁺² ion has one unpaired hole (positive charge) which can occupy two degenerate states, and in such cases, the structure is expected to undergo a Jahn-Teller (J-T) distortion. Briefly, when a hole (or electron) occupies a 2-fold degenerate state on an atom (here Cu), a distortion of the cage of surrounding oxygen (O) atoms will split the degeneracy and the hole (or electron) will then occupy the lower of these two energies. Typically, as for a class of materials called manganites, there are two long metal-oxygen bonds and four shorter bonds. Such a distortion would make the g-vector anisotropic and lead to an orthorhombic distortion of the lattice – and to a preferred orientation of the Cu magnetic moments at low T; however neither is observed in ESR and neutron scattering studies for the stoichiometric material.

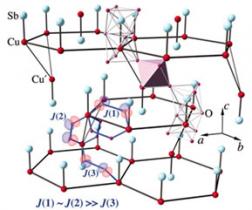
In slightly non-stoichiometric samples however (Sb:Cu ratio differs from 2:1 by 10%), an orthorhombic structural distortion is observed, consistent with the expected J-T distortion, and the g-value becomes quite anisotropic. This raises the question - is there still a J-T distortion about the Cu atoms that is somehow "averaged out" in the stoichiometric lattice? In addition to a possible J-T distortion in the stoichiometric material, another question arises from the crystal structure obtained from diffraction studies of single crystal samples. In the hexagonal (space group P6₃/mmc) one of the sites in the unit cell is shared 50:50 by Sb and Cu and referred to as Cu/Sb(2) (half of the Sb also occupy a different site, Sb(1)). The Cu/Sb(2) atoms occur in dumbbell pairs, oriented along the c-axis, and if the occupation were random there could be Cu-Cu, Sb-Sb and Cu-Sb pairs. Diffraction studies cannot determine what types of dumbbell are present. Because of the difference in charge (Cu⁺², Sb⁺⁵) the Cu-Sb dumbbell would have an electric dipole moment, and it is important to determine if a significant fraction of Cu-Sb dumbbells is present. Note that several measurements indicate that the sample is not ferroelectric (i.e. there is no net electric dipole moment); thus if Cu-Sb dumbbells are present, they must alternate throughout the lattice so as to cancel out any net electric polarization.

More details about this unusual spin system can be found in the highlight published in Science. Here I focus on the local structure issues that were probed using EXAFS. Note that EXAFS is a very fast local probe, much faster than phonon frequencies, and will see all lattice distortions including fluctuating J-T distortions.

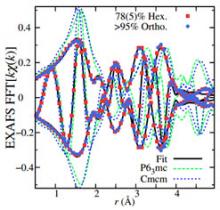Figure 1 The EXAFS Cu K-edge r-space data for the hexagonal (red squares) and orthorhombic (blue circles) samples at 10 K. The local structure about Cu is nearly identical in the two samples although the long range order is different. Simulations based on the hexagonal (green dash) or orthorhombic (blue dash) structures do not describe the EXAFS data very well; in particular the experimental amplitude for the Cu-O peak near 1.6 Å is much lower than the simulations while the experimental Cu-Sb/Cu peak near 2.5 Å is significantly larger than the simulations.

The Cu K-edge EXAFS r-space plots, shown in Fig. 1 (Fig 2F of paper), show that the hexagonal (stoichiometric) and orthorhombic (slightly nonstoichiometric) samples appear nearly identical at the local level. More importantly, simulations using several similar crystal structures (space groups P6₃/mmc, P6₃/mc, or Cmcm) all showed that the Cu-O nearest neighbor pair-distribution is not strongly disordered; however, the amplitude of the Cu-O peak observed experimentally is considerably smaller than the simulations, indicating significant Cu-O disorder. In contrast for the Sb K-edge EXAFS (see paper supplement) the Sb-O pair distribution function is sharp and the amplitude high.

Fits of the Cu-O peak to a J-T split model show a significant J-T splitting of the Cu-O bond lengths by 0.23 Å, for both the hexagonal and orthorhombic samples. Thus at the local level, the J-T splitting is indeed present in the sample that is on average, hexagonal, but this distortion must be averaged out in other types of measurements. Two possibilities exist; the J-T distortion may be fluctuating very rapidly - faster for example than ESR time scales, so that the ESR line is motionally narrowed. A second possibility is that the J-T distortions are static but randomly arranged at the nanoscale, so that on average the lattice appears hexagonal. It could also be a combination of time and spatial averaging but it is difficult to separate these possibilities.

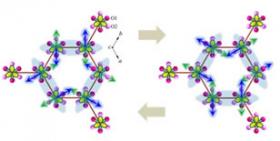
The second peak in the Cu EXAFS data (Fig. 1) corresponds to a Cu-Cu/Sb pair. Fits of this peak to a sum of Cu-Cu and Cu-Sb peaks show that this second peak corresponds primarily to (well-ordered) Cu-Sb pairs although we cannot exclude the possibility of a few percent of Cu-Cu pairs. Similarly in the Sb EXAFS data, the second sharp peak is primarily an Sb-Cu peak. This important result plus diffuse scattering in diffraction studies and no net electric polarization, lead to the honeycomb lattice of alternating Cu-Sb dumbbells shown in Fig. 2 (Fig. 1A in paper). The 3-D honeycomb lattice leads to triangles of Cu atoms coupled via J1 and J2 as shown in Fig. 1. The J1/J2 interactions tend to align the Cu moments anti-parallel but this cannot be achieved simultaneously for three moments on a triangle - this leads to frustration for the Cu spin orientation. Consequently, the Cu spins on a hexagon within the honeycomb lattice can have different, energetically equivalent orientations as shown in Fig. 3.

Figure 2 The Cu-Sb dumbbell lattice for Ba3CuSb2O9; Ba atoms excluded for clarity. The Cu-Sb dumbbells must be randomly aligned up and down along the c-axis to eliminate any net electric polarization. EXAFS showed that the dumbbells were primarily Cu-Sb, with few Cu-Cu or Sb-Sb dumbbells. Credit: H Sawa, Nagoya University

Figure 3 Two sets of Cu spin orientations on a hexagon from the honeycomb lattice; either the “green” or “blue” set of spins describe the magnetic arrangement at a given time. The right side shows a rotated possibility.  These have the same energies but quite different spin orientations;  consequently, the spins are "frustrated" as to which orientation they should take. Credit: Satoru Nakatsuji, University of Tokyo

In summary the discovery of quantum spin-liquid behavior in Ba₃CuSb₂O₉ provides a new opportunity to study this unusual spin-liquid state, and provides guidance in searching for other spin-liquid systems. The fact that the magnetic system remains liquid-like in spite of large interaction energies and significant local distortions is surprising, and indicates that the earlier perception, that the quantum spin-liquid state is unstable in the presence of distortions, needs to be revised. It also highlights the need for a better understanding of how different measurements average over some region in space or some interval in time and leads to a new challenge – how can these two types of averages be separated?