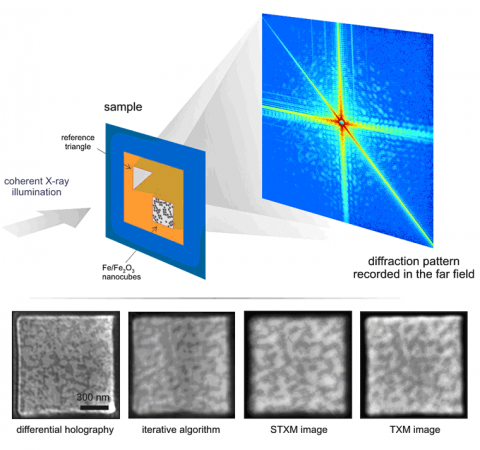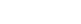
Coherent diffractive imaging (CDI) is an x-ray microscopy technique that takes advantage of the coherence property of modern x-ray sources. Its resolution is in principle only limited to the wavelength of the x-rays being used [1]. Instead of using imaging optics such as lenses to form a magnified image, CDI tries to interpret the recorded coherent diffraction pattern and to obtain a numerical image reconstruction of the scattering object. Fourier transform holography is a particularly straight forward method for generating coherent diffraction patterns that are easy to interpret [2]. By introducing a nanoscale reference scatterer next to the object of interest and measure the x-ray interference pattern, an image reconstruction can be directly obtained by simply Fourier transforming the measured diffraction intensity distribution.
Previous Fourier transform holography experiments used small pinholes as the reference. The resolution was determined by the size of the reference pinhole. Very small pinholes are not only difficult to fabricate, but also lead to diminishing signal-to-noise ratio.
We have recently demonstrated at SSRL Beamline 13-3 that by using extended reference structures with sharp corners, higher resolution can be achieved with the same reference fabrication tool.
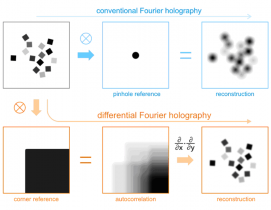
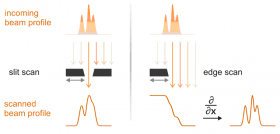
The concept [3, 4] is very much similar to the "edge scan" method that is widely used for determining the profile of a small beam, as schematically illustrated in Figure 1. The image reconstruction from conventional Fourier holography can be viewed as a convolution of the ideal image with the reference. For differential holography technique, the convolution happens between the ideal image and a sharp corner that is used as the reference. The additional step of differential operation is able to deliver a much sharper image, as shown in Figure 2.
In the actual experiment at SSRL, we imaged iron/iron-oxide nanocubes 18 nm in size dispersed on a silicon nitride membrane. A resolution of 16 nm was obtained using a triangular holographic reference, a big improvement comparing with the 30 nm resolution achievable with conventional x-ray Fourier transform holography using pinhole references. The image reconstruction also compares favorably with alternative x-ray microscopy methods as shown in Figure 3. Moreover, the differential method shows improved robustness against the missing central part of the diffraction pattern, making it potentially a powerful technique for performing lensless holographic imaging experiments at LCLS.
- J. Miao, et al., "Extending the methodology of x-ray crystallography to allow imaging of micrometer-sized non-crystalline specimens", Nature 400, 342 (1999).
- S. Eisebitt, et al., "Lensless imaging of magnetic nanostructures by x-ray spectroholography", Nature 432, 885 (2004).
- S. G. Podorov, et al., "A non-iterative reconstruction method for direct and unambiguous coherent diffractive imaging", Opt. Express 15, 9954 (2007).
- M. Guizar-Sicairos and J. R. Fienup, "Holography with extended reference by
D. Zhu, et. al. "High-resolution x-ray lensless by differential holography encoding", Phys. Rev. Lett. 105, 043901 (2010).