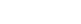Stanford Synchrotron Radiation Lightsource

It has recently been proposed that insulators with large band gap and strong spin-orbit coupling can host a new phase of quantum matter called a topological insulator [1,2]. This exotic phase of matter is a subject of intense research because it is predicted to give rise to dissipationless spin currents [3], quantum entanglements and novel macroscopic behavior that obeys axionic electrodynamics rather than Maxwell's equations [4]. Unlike ordinary quantum phases of matter such as superconductors, magnets or superfluids, topological insulators are not described by a local order parameter associated with a spontaneously broken symmetry but rather by a quantum entanglement of its wave function, dubbed topological order. In a topological insulator this quantum entanglement survives over the macroscopic dimensions of the crystal and leads to surface states that have unusual spin textures.

Figure 1. (A) Schematic of the 1D edge states in a 2D topological insulator. The red and blue curves represent the edge current with opposite spin character. (B) Schematic of the 2D surface states in a 3D topological insulator.

Topologically ordered phases of matter are extremely rare and are experimentally challenging to identify. The only known example was the quantum Hall effect discovered in the 1980s by von Klitzing (Nobel Prize 1985). It was identified by measuring a quantized magneto-transport in a two-dimensional electron system under a large external magnetic field at very low temperatures, which is characterized by robust conducting states localized along the one-dimensional edges of the sample. Two-dimensional topological insulators, on the other hand, are predicted to exhibit similar edge states even in the absence of a magnetic field because spin-orbit coupling can simulate its effect (Fig.1A) due to the relativistic terms added in a band insulator's Hamiltonian.

Remarkably, three-dimensional topological insulators, an entirely new state of matter with no charge quantum Hall analogue, are also postulated to exist. And its topological order or exotic quantum entanglement is predicted to give rise to unusual conducting two-dimensional surface states (Fig.1B) that have novel spin-selective energy-momentum dispersion relations. Utilizing state-of-the-art angle-resolved photoemission spectroscopy (ARPES) at Beam Line 5-4 of SSRL, an international collaboration led by scientists from Princeton University have studied the electronic structure of insulating alloys of bismuth and antimony. By a systematic tuning of the incident photon energy, they were able to separate the signal from both surface and bulk states, and thereby confirmed that these insulating alloys realized a three-dimensional topological insulating phase. Spin detection was carried out separately at the COPHEE beam line of the Swiss Light Source.

Remarkably, three-dimensional topological insulators, an entirely new state of matter with no charge quantum Hall analogue, are also postulated to exist. And its topological order or exotic quantum entanglement is predicted to give rise to unusual conducting two-dimensional surface states (Fig.1B) that have novel spin-selective energy-momentum dispersion relations. Utilizing state-of-the-art angle-resolved photoemission spectroscopy (ARPES) at Beam Line 5-4 of SSRL, an international collaboration led by scientists from Princeton University have studied the electronic structure of insulating alloys of bismuth and antimony. By a systematic tuning of the incident photon energy, they were able to separate the signal from both surface and bulk states, and thereby confirmed that these insulating alloys realized a three-dimensional topological insulating phase. Spin detection was carried out separately at the COPHEE beam line of the Swiss Light Source.

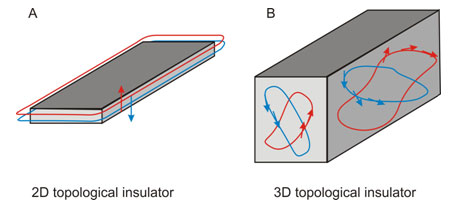
The remarkable property of the surface states of a 3D topological insulator is that its Fermi surface supports a geometrical quantum entanglement phase, which occurs when the spin-polarized Fermi surface encloses the Kramers' points and on the surface Brillouin zone an odd number of times in total (Fig.2B). ARPES intensity map of the (111) surface states of bulk insulating Bi_1-xSb_x (Fig.2A) shows that a single Fermi surface encloses . However, determination of the degeneracy of the additional Fermi surface around requires a detailed study of its energy-momentum dispersion. ARPES spectra along the - direction (Fig.2C) reveal that the Fermi surface enclosing is actually composed of two bands, therefore two Fermi surfaces enclose , leading to a total of seven and Fermi surface enclosures.

Figure 2. (A) ARPES surface state (SS) Fermi surface of insulating Bi_1-xSb_x showing spin polarization directions as indicated by red and blue arrows. (B) Schematic of the SS Fermi surface of a 3D topological insulator. (C) ARPES energy-momentum dispersion of the surface states. The shaded areas denote the bulk bands while the dashed white lines are guides to the eye for surface state dispersions.

These results constitute the first direct experimental evidence of a topological insulator in nature which is fully quantum entangled. The observed spin-texture in BiSb is consistent with a magnetic monopole image field beneath the surface as predicted in theory [5]. It shows that spin-orbit materials are a new family in which exotic topological order quantum phenomena, such as dissipationless spin currents and axion-like electrodynamics, may be found without the need for an external magnetic field. The results presented in this study also demonstrate a general measurement algorithm of identifying and characterizing topological insulator materials [6,7] for future research which can be utilized to discover, observe and study other forms of topological order and quantum entanglements in nature. A detailed study of topological order and quantum entanglement can potentially pave the way for fault-tolerant (topological) quantum computing.

This work was supported by the DOE, NSF and Princeton University.