
Since the discovery of high-temperature superconductor by Bednorz and Müller in
1986, this field has become one of the most important research topics in solid
state physics. In the past 20 years many unconventional properties have been
discovered in this new class of materials. These have challenged our
conventional wisdom and driven the development of many novel theories. Among
these discoveries, the most mysterious is probably the pseudogap phenomena: it
has been observed that there is an energy gap above the superconducting
transition temperature (TC) that persists over a wide range of
temperatures and chemical compositions [1]. This peculiar
behavior appears to be very different from a conventional superconductor. Here
the electrons form so-called "Cooper pairs", which manifests itself as an
energy gap in many spectroscopic measurements. This energy gap, known as
superconducting gap, appears only below TC where the electrical
resistance also vanishes (hence the name 'superconductor'). This important
difference has stimulated lots of debate in the search of understanding
high-TC superconductivity on questions such as: "What is the
pseudogap?" and "What is its relation to superconducting gap and
superconductivity at high temperature?"
Early measurements of the energy gap via scanning tunneling
spectroscopy (STM) and angle-resolved photoemission spectroscopy (ARPES) near
the Brillouin zone boundary (antinodal region) suggested a smooth transition
from a pseudogap to a superconducting gap. Hence, the pseudogap state was
interpreted as the precursor state of superconducting state but without the
phase coherence of the Cooper pairs (a necessary condition for
superconductivity). On the other hand, other measurements such as Andreev
reflection and time-resolved spectroscopy, observed a superconducting gap that
appears at TC as the temperature is lowered, similar to the behavior of the
conventional superconductors. In this interpretation, the pseudogap and
superconducting gap are two different energy scales representing different
ordering phenomena. To resolve this contradiction and gain further insight of
pseudogap phenomena, researchers Wei-Sheng Lee and Inna Vishik along with their
co-workers in Prof. Zhi-Xun Shen's group at Stanford University, have recently
made an important discovery about the temperature dependence of the gap along
the Fermi surface. These results provide more crucial evidence of the
coexistence of two energy gaps and clarify the relationship between them.
The measurements were performed at SSRL beamline 5-4 using the state-of-the-art
ARPES system. The excellent beam stability and high data acquisition efficiency
allow Lee et al. to measure the gap of underdoped superconducting cuprates,
Bi2212, along Fermi surface with ultrahigh resolution (3-5meV) and
unprecedented detail in both momentum space and temperature. The surprising
results obtained from these measurements allowed them to address the issue of
pseudogap and superconducting gap in a way missed by the previous ARPES
measurements on the same topic.
|  |
|
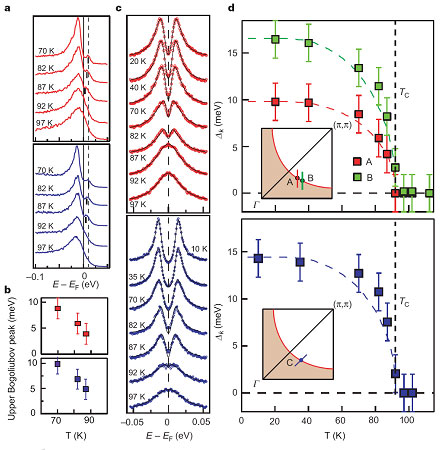
Figure 1.
Detailed temperature dependence of the superconducting gap near the nodal
region of underdoped Bi2212 (Tc592 K) measured under two different
experimental configurations. Data shown in each upper panel were measured along
cuts parallel to the (p,0)-(p,p) direction, using 22.7-eV photons and an energy
resolution of 5meV. The data in each lower panel were measured along cuts
parallel to the (0,0)-(p,p) direction, using 7-eV
photons and an energy resolution of 3.2meV. (a) Temperature dependence of raw
EDCs near the Fermi-surface crossing points A (upper panel) and C (lower
panel). (b) Temperature dependence of the peak position of the thermally
populated upper Bogoliubov band in the raw spectra shown in a, which
extrapolates to zero near Tc. (c) Temperature dependence of the symmetrized
EDCs at Fermi-surface crossing points A (upper panel) and C (lower panel)
superimposed on their fit (black curves) to the phenomenological model. (d),
Temperature dependence of the fitted gap size at Fermi-surface crossing points
near the node, as indicated in the insets. | |
The biggest surprise is the temperature dependence of the gap near the diagonal
of the Brillouin zone, where the gap is in general small and has been
overlooked in the previous measurements. As shown in the symmetrized spectra
(Fig. 1(c)), the gap apparently vanishes at the superconducting transition
temperature in a BCS-like fashion. This is confirmed by fitting the gap to a
phenomenological model (Fig. 1(d)). This behavior is in stark contrast to the
gap at the antinodal region, where the gap magnitude remains almost unchanged
across Tc and smoothly evolves into pseudogap. Further evidence of
such a temperature dependence can also be found in the raw spectra shown in
Fig. 1(a). Due to significant thermal population above the Fermi energy
(EF) at higher temperatures, the upper branch of the Bogoliubov
dispersion, which represents a mixture of electron and hole states and is a
hallmark of the superconducting state, can be seen as a small peak above
EF (indicated by the short bars in Fig. 1(a)). As the temperature
approaches TC, its peak position (Fig. 1(b)) moves closer to
EF, suggesting a
rapid decrease of the gap. The Bogoliubov dispersion eventually disappears
above TC when no gap can be detected at this momentum position,
consistent with the conventional BCS superconductor.
As also described in their paper published in Nature, the different
temperature dependence at different momentum positions along the Fermi surface
leads to a highly nontrivial temperature dependent evolution of the gap
function. This may contain important information to further reveal the
relationship between the superconducting gap and pseudogap. In any case,
together with their previous work on heavily underdoped Bi2212 system published
in Science last year [2], it is now well established
that the superconducting gap and pseudogap are two distinct energy scales in
the single-particle spectrum. This should provide an important step toward
unveiling the mystery of the pseudogap phenomena.
Primary Citation:
W. S. Lee, I. M. Vishik, K. Tanaka, D. H. Lu, T. Sasagawa, N. Nagaosa, T. P.
Devereaux, Z. Hussain and Z.-X. Shen, Nature 450, 81 (2007)
References:
-
T. Timusk, B. Statt, Rep. Prog. Phys. 62, 61 (1999).
-
K. Tanaka et al., Science 314, 1910 (2006).
|
| PDF
Version | | Lay Summary | |
Highlights Archive
|
| SSRL is supported
by the Department of Energy, Office of Basic Energy Sciences. The SSRL
Structural Molecular Biology Program is supported by the Department of Energy,
Office of Biological and Environmental Research, and by the National Institutes
of Health, National Center for Research Resources, Biomedical Technology
Program, and the National Institute of General Medical Sciences. |
|


