
X-ray free-electron lasers (XFELs) will produce photon pulses with a unique and
desirable combination of properties. Their short X-ray wavelengths allow
penetration into materials and the ability to probe structure at and below the
nanometer scale. Their ultra-short duration gives information about this
structure at the fundamental time-scales of atoms and molecules. The extreme
intensity of the pulses will allow this information to be acquired in a single
shot, so that these studies can be carried out on non-repeatable processes or
on weakly-scattering objects that will be modified by the pulse. A fourth
property of XFEL pulses is their high transverse coherence, which brings the
promise of decades of innovation in visible optics to the X-ray regime, such as
holography, interferometry, and laser-based imaging. Making an effective use
of XFEL pulses, however, will benefit from innovations that are new to both
X-ray science and coherent optics. One such innovation is the new method of
time-delay X-ray holography [i], recently demonstrated at the FLASH FEL at DESY
in Hamburg, to measure the evolution of objects irradiated by intense pulses.
One of the pressing questions about the high-resolution XFEL imaging and
characterization of non-periodic or weakly-scattering objects is the effect of
the intense FEL pulse on the object, during the interaction with that pulse.
The method of single-particle diffraction imaging [ii] requires a stream of
reproducible particles (e.g. a protein complex or virus) inserted into the
beam, whereby a coherent X-ray diffraction pattern is recorded. The pulse will
completely destroy the object, but if the pulse is short enough the diffraction
pattern will represent the undamaged object. This ultrafast flash imaging was
demonstrated at the FLASH FEL using test objects that included microfabricated
patterns in silicon nitride foils [iii]. Those experiments showed that no
damage occurred during the 30 fs duration pulse. However, in those experiments
the imaging resolution was limited by the long 32 nm wavelength at which the
facility was then operating. We wished to dramatically increase our
sensitivity to the particles' explosions, to be able to increase the
understanding of the dynamics of particles and predict the imaging performance
at XFELs such as the LCLS. This was done in two ways in a single experiment:
by holographically measuring the time evolution of the particle at times after
the pulse had pass through the object; and by making an interferometric
measurement of the change in the optical path through the object. The
experimental technique, time-delay holography, achieved a time resolution
better than 3 fs, and a phase sensitivity of better than 3°, or a sensitivity
of < 3 nm of the expansion of the particles.
The idea behind time-delay holography is to use the same pulse that initiated
the interaction with an object to probe that object at a later time. This was
achieved simply by placing a mirror behind the object to send the pulse back on
the object a second time. The time delay is easily set by the distance between
the mirror and the object. This geometry is in fact the same as the
`dusty-mirror' experiment that was first carried out by Newton. Newton's
observations of light and dark rings formed when reflecting a shaft of sunlight
from a dusty mirror back through a hole in a screen, was one of the earliest
recorded of interference. The explanation for the effect was not forthcoming
until a century later when Thomas Young explained these as interferences of
waves traveling along two paths: 1) incident on the mirror, scattering from a
dust particle before passing through the mirror glass and reflecting its back
surface (which was silvered with mercury); and 2) first passing through the
thickness of the glass of the mirror, reflecting, and then scattering from the
particle on the way out. Further, experiments, performed with clouds of wig
powder, confirmed Young's hypothesis.
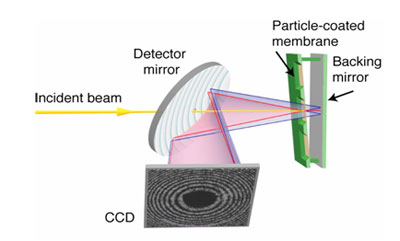 |
X-rays from the FLASH FEL are focused on to a 'dusty mirror' consisting of
particles on a membrane sandwiched closely to a multilayer backing mirror. An
ultrashort pulse hits the particles twice: on the way in and after reflecting
from the mirror. The two scattered waves interfere on the CCD to form a
hologram that encodes the change in the particle in the brief time that the
light was reflected back.
| |
We manufactured a multilayer with a broad reflectivity rocking curve to use as
the object backing mirror. Both the direct beam and the wide-angle scattered
wave from the object reflect from this mirror. The reflected direct beam, on
hitting the object for a second time, creates another scattered wave. This
wave, however, carries structural information about the object at a later time
than the initial interaction. If the object had expanded in this time, for
example, the second diffracted wave would be more forward-peaked. The two
scattered waves (the first from the undamaged object, the second a well-defined
time later) propagate together and are detected on a CCD. Now, even though the
pulse hit the object at two distinct times, the two waves generated by these
events do travel together and interfere with each other at the detector. This
interference is dominated by a distinct ring pattern, which is the interference
of two spherical waves that are longitudinally displaced. With many objects
placed in the beam, each one generates an interference pattern which then
coherent adds with all others, modulating the ring pattern with a speckle
pattern. The ring pattern accurately encodes the distance between the
spherical waves, which can be determined to high accuracy. From this distance
the delay between the events can be determined to better than 3 fs.
The sample in our experiments consisted of an array of hundreds of silicon
nitride membrane windows on which 140-nm diameter polystyrene spheres were
placed. This was sandwiched against the multilayer backing mirror, positioned
with a slight wedge to be able to vary the delay simply by moving to different
membrane windows. The smallest gap was about 50 micron, to give a delay of
about 300 fs, and the longest gap gave a delay of 8 ps. Each window gave the
opportunity for several separate exposures. Even though the 20-micron-wide
focused FEL pulse ablated a crater in the backing mirror and melted a hole in
the silicon nitride, the entire window did not shatter so we could simply move
to a new spot.
We consider the recorded diffraction pattern as a hologram, as it consists of
the interference of a known reference wave (the undamaged object) with an
unknown object wave (the object undergoing an explosion). The holograms were
initially analyzed by considering the intensity of the interference between
these waves as a function of scattering angle, or momentum transfer q. This
was compared with calculated patterns, using a hydrodynamic model [iv]. We see
that, as predicted, the patterns become narrower and more forward peaked as the
time delay is increased beyond 3.8 ps. This suggests that in real space the
objects are indeed expanding following the interaction. Furthermore, the
evolution of the structure factor of the polystyrene sphere is in good
agreement with our calculations to the longest-measured delays of 8 ps where
the sphere has approximately doubled in size.
|
 |
|
A time-delay hologram recorded for a delay of 348 fs for 140-nm diameter
polystyrene spheres. The ring pattern encodes both the delay and the change in
phase of the pulse as it travels through the exploding object. Holograms
recorded at different delays reveal the FEL-induced explosion of the spheres.
|
At delays shorter than 3 ps the expansion of the sphere was less than the
transverse spatial resolution of 60 nm and hence could not be observed.
However, changes in the optical properties of the sphere could be observed for
delays even shorter than 1 ps. This is due to the interferometric nature of
the measurement. The wave scattering from a polystyrene sphere is phase
shifted by an amount that depends on the sphere's refractive index and (at low
q) its thickness. If these properties change by the time the pulse returns to
the sphere then the phase shift on scattering the second time will be different
to the first. This relative phase shift will cause a change in the ring fringe
pattern of the hologram. For example, a change in the phase shift by
p (half a
wave) would reverse the contrast of the fringes by causing constructive
interference where there would have been destructive interference. The
relative phase can thus be determined from the positions of the ring maxima and
minima. We observed an increase in the phase shift with time delay and for
increasing pulse fluence. At a delay of 350 fs the change in phase shift was
equivalent to an increase of the optical path by less than 1/50th of a
wavelength. Since the refractive index is negative (and close to unity) this
corresponds to a reduction of material projected through the ball as would
occur if the sphere expanded in all directions by 3 nm.
The experiment achieved this high level of precision in space and time without
any complex optics or diagnostics, simply by utilizing the coherence of the
pulse and the geometry of the `dusty mirror.' Other geometries are planned in
for future X-ray FELs, using grazing geometries for shorter X-ray wavelengths
and shorter time delays. The technique should be applicable to the
high-resolution measurement of shocks, crack formation, ablation, melting,
ultrafast phase transitions, and plasma formation.
Acknowledgments
Experiments were carried out at the FLASH FEL in DESY, Hamburg, by a
collaboration of scientists from LLNL, Uppsala University, SLAC, LBNL, and TU
Berlin. This work was performed under the auspices of the U.S. Department of
Energy by Lawrence Livermore National Laboratory under Contract
DE-AC52-07NA27344.
Primary Citation
H. N. Chapman, S. P. Hau-Riege, M. J. Bogan, S. Bajt, A. Barty, S. Boutet, S.
Marchesini, M. Frank, B. W. Woods, W. H. Benner, R. A. London, U. Rohner, A.
Szöke, E. Spiller, T. Möller, C. Bostedt, D. A. Shapiro, M. Kuhlmann, R.
Treusch, E. Plönjes, F. Burmeister, M. Bergh, C. Caleman, G. Huldt, M. M.
Seibert and J. Hajdu, "Femtosecond Time-Delay X-ray Holography",
Nature 448, 676 (2007)
References
i. H.N. Chapman et al., "Femtosecond time-delay x-ray holography," Nature
448, 676-679 (2007).
ii. R. Neutze, R. Wouts, D. van der Spoel, E. Weckert, and J. Hajdu, "Potential
for biomolecular imaging with femtosecond x-ray pulses," Nature 406,
753-757 (2000).
iii. H.N. Chapman et al., "Femtosecond diffractive imaging with a soft-x-ray
free-electron laser," Nat. Phys.,2, 839-843 (2006).
iv. S.P. Hau-Riege, R.A. London, H.N. Chapman, and M. Bergh, "Soft-x-ray
free-electron-laser interaction with materials," Phys. Rev. E 76, 046403
(2007).
|
| PDF
Version | | Lay Summary | |
Highlights Archive
|
| SSRL is supported
by the Department of Energy, Office of Basic Energy Sciences. The SSRL
Structural Molecular Biology Program is supported by the Department of Energy,
Office of Biological and Environmental Research, and by the National Institutes
of Health, National Center for Research Resources, Biomedical Technology
Program, and the National Institute of General Medical Sciences. |
|



