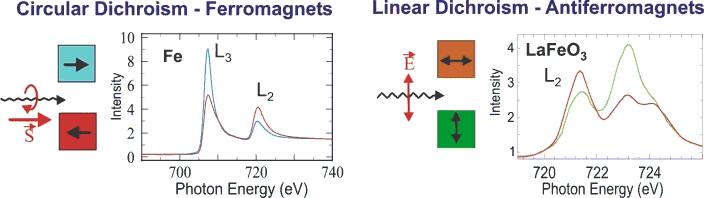
Fig. 1 (click to enlarge): Illustration of the size of magnetic dichroism effects. Note that the XMLD effect is large only in cases where the absorption edge exhibits multiplet structure.
Many different metals like Fe, Co or Ni are ferromagnetic and their magnetic properties are best studied with X-Ray Magnetic Circular Dichroism (XMCD) spectroscopy, while the oxides are usually antiferromagnetic and are studied with X-Ray Magnetic Linear Dichroism (XMLD) spectroscopy. Both XMCD and XMLD effects are large as illustrated in Fig. 1, and in the following we shall discuss the two techniques in detail.
Fig. 2 (click to enlarge): Electronic transitions in conventional L-edge x-ray absorption (a), and x-ray magnetic circular x-ray dichroism (b,c), illustrated in a one-electron model. The transitions occur from the spin-orbit split 2p core shell to empty conduction band states. In conventional x-ray absorption the total transition intensity of the two peaks is proportional to the number of d holes (first sum rule). By use of circularly polarized x-rays the spin moment (b) and orbital moment (c) can be determined from linear combinations of the dichroic difference intensities A and B, according to other sum rules.
The concepts of XMCD spectroscopy, pioneered by Gisela Schütz et al. in 1987, are illustrated in Fig. 2. The first x-ray absorption sum rule links the total intensity of the L3 and L2 resonances with the number N of empty d states (holes). The d valence shell can hold up to 10 electrons which are filled into band states up to the Fermi level and the number of filled states is therefore 10 -N. For a magnetic material the d shell has a spin moment which is given by the imbalance of spin-up and spin-down electrons or equivalently (except for the sign) by the imbalance of spin-up and spin-down holes. In order to measure the difference in the number of d holes with up and down spin, we need to make the x-ray absorption process spin dependent. This is done by use of right or left circularly polarized photons which transfer their angular momentum to the excited photoelectron.
The photoelectron carries the transferred angular momentum as a spin or an angular momentum, or both (Stohr & Wu). If the photoelectron originates from a spin-orbit split level, e.g. the p3/2 level (L3 edge), the angular momentum of the photon can be transferred in part to the spin through the spin-orbit coupling. Right circular photons (RCP) transfer the opposite momentum to the electron as left circular photons (LCP) photons, and hence photoelectrons with opposite spins are created in the two cases. Since the p3/2 (L3) and p1/2 (L2) levels have opposite spin-orbit coupling, the spin polarization will be opposite at the two edges. In the absorption process, "spin-up" and "spin-down" are defined relative to the photon helicity or photon spin.
Since spin flips are forbidden in electric dipole transitions, spin-up (spin-down) photoelectrons from the p core shell can only be excited into spin-up (spin-down) d hole states. Hence the spin-split valence shell acts as a detector for the spin of the excited photoelectron and the transition intensity is simply proportional to the number of empty d states of a given spin. The quantization axis of the valence shell "detector" is given by the magnetization direction. The size of the dichroism effect scales like cos θ, where θ is the angle between the photon spin and the magnetization direction. Hence the maximum dichroism effect (typically 20%) is observed if the photon spin direction and the magnetization directions are parallel and anti-parallel as shown on the left side of Fig. 1. When the photon spin and the magnetization directions are perpendicular the resonance intensities at the L3 and L2 edges lie between those obtained for parallel and anti-parallel alignments.
The L3 and L2 resonance intensities and their differences for parallel and anti-parallel orientation of photon spin and magnetization directions are quantitatively related by sum rules to the number of d holes and the size of the spin and orbital magnetic moments. Angle dependent measurements in external magnetic fields give the anisotropies of the spin density and orbital moment. For a review see IBM. J. Res. Develop. 42, 73 (1998) and J. Magn. Magn. Mater. 200, 470 (1999).
Fig. 3 (click to enlarge): Origin of XMLD for NiO. On the left we show the electronic configurations involved in the x-ray absorption process. In the ground state there are two d holes (d2 hole configuration) and their energy levels are determined by multiplet and crystal field effects. In the final state, a 2p hole is created by x-ray absorption and one d hole is filled by the excited electron. The resulting pd hole configuration again gives rise to multiplet splitting and the XAS spectrum reflects the multiplet structure. In the paramagnetic state the absorption spectrum of NiO does not exhibit a polarization dependence because of cubic symmetry. In the antiferromagnetic state the spin-orbit coupling leads to a distortion of the charge density and an XMLD effect is observed.
XMLD spectroscopy was pioneered by Gerrit van der Laan et al. in 1986. The electric field vector E of linearly polarized x-rays acts as a search light for the number of valence holes in different directions of the atomic volume. In most cases the anisotropy of the charge in the atomic volume is caused by an anisotropy in the bonding, i.e. by the electrostatic potential. In the absence of spin order, linear dichroism NEXAFS spectroscopy can only determine charge order in systems where the absorbing atom has lower than cubic symmetry. However, in the presence of spin order the spin-orbit coupling leads to preferential charge order relative to the spin direction even in cubic systems. This effect is the basis for the determination of the spin axis in ferromagnetic and especially antiferromagnetic systems by means of x-ray magnetic linear dichroism (XMLD) spectroscopy. Since the electric field vector oscillates in time along an axis and the radiation may be absorbed at any time, linearly polarized x-rays are only sensitive to axial not directional properties. Hence one can determine the orientation of the antiferromagnetic or ferromagnetic axis, but the spin direction itself cannot be determined.
Fig. 3 illustrates the origin of the XMLD effect in NiO. Because of the cubic symmetry of the NiO lattice the charge distribution around the atoms is nearly spherical and no linear dichroism effect exists above the Néel temperature (520 K), where NiO is paramagnetic. At room temperature, NiO is antiferromagnetic and the Ni spins are oriented in the (1,1,1) plane along three possible directions in the fcc lattice. There is no net magnetic moment because an equal number of spins point into opposite directions, so only a preferential magnetic axis exists. The alignment of the local atomic spins along this axis breaks the cubic symmetry of the charge through the spin orbit coupling. As a consequence the charge exhibits a small anisotropy in the unit cell, i.e. it is no longer spherical but shows an ellipse-like distortion about the magnetic direction. This charge anisotropy leads to an asymmetry of the x-ray absorption signal through the search light effect.
The maximum XMLD difference is obtained for E parallel versus E perpendicular to the magnetic axis, as shown in Fig. 3. In contrast to the XMCD effect the XMLD effect has a cos2θ dependence, where θ is the angle between E and the magnetic axis. In general, the XMLD effect is small in 3d metals owing to the small size of the spin orbit interaction and the large band width, resulting in a small charge anisotropy when the d states are summed over the Brillouin zone. However, a sizeable XMLD effect (of order 10-30%) may be observed in the presence of multiplet splitting. At a particular multiplet energy only selected d valence states are probed through matrix element effects that enhance the XMLD effect. In a simple picture we can view each multiplet as a strongly coupled spin-orbit state whose spatial extent is non-spherical, giving rise to the large XMLD effect. In Fig. 3 the XMLD effect is especially visible at the Ni L2-edge where a sizeable difference is observed for E parallel (green) versus perpendicular (red) to the magnetic axis. Since x-ray linear dichroism can arise from electric and magnetic asymmetries, care needs to be taken to distinguish magnetic order effects from ligand field effects. This is typically done through temperature dependent measurements.