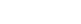
The intricacy of structure determination due to the lost phase information in diffraction measurements can be downsized to a manageable problem by labeling the unknown specimen with a few heavy atoms that serve as reference scatterers. In this way, multiple-wavelength anomalous diffraction (MAD) phasing has revolutionized macromolecular structure determination on atomic length scales and has become a well established technique in x-ray crystallography with dedicated synchrotron beamlines.[1] An important prerequisite for conventional MAD is the periodicity of the sample which requires for assembling the biological molecules into a crystal.
In this work, the methodology of MAD is extended to non-periodic structures using the concept of coherent x-ray imaging, cf. Figure 1. The solution of the phase problem is demonstrated in a proof of principle experiment by a combination of two resonantly recorded scattering or speckle patterns at the carbon K edge. This new approach merges iterative phase retrieval [2] and x-ray holography approaches [3] and facilitates unique and rapid reconstructions. The inherent resonant aspect provides sensitivity to the elemental, chemical and magnetic state that further renders lensless MAD imaging widely applicable to a broad range of nanostructures with in principle wavelength limited spatial resolution.
The experiment was carried out on the soft x-ray coherent scattering Beamline 13-3 of SSRL. The speckle patterns were recorded from dispersed polysterene spheres on a silicon nitride membrane with a gold aperture. The scattered wave field consists out of resonant and nonresonant components and the interference of both is recorded with an array detector in the far-field of the sample. The strong change of the optical constants or atomic scattering factors of matter across resonances at the threshold of core electron excitation energies allows for defining a generalized reference wave as the energy-dependent part which resonantly phases the nonresonant scattered wave emerging from other parts of the sample.
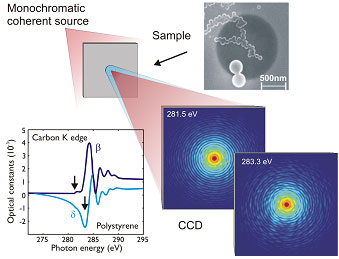
The interference patterns reveal remarkable changes at nearly the same photon energy reflecting the changes in the optical constants. The optical constants have been determined by measuring the absorption of the sample. Given the optical constants and applying the MAD concept the energy-dependent interference patterns have been decomposed into resonant and non-resonant amplitudes and their relative phases (MAD phases). The non-resonant amplitude reproduces an Airy pattern from the circular Au aperture while the resonant part shows a speckle pattern from the local arrangement of the polysterene spheres.
Two images, a resonant image of the polysterene spheres and a nonresonant image of the aperture, are simultaneously reconstructed by disentangling the MAD
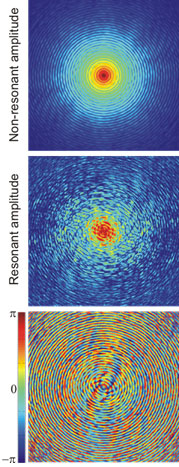
phases into resonant and nonresonant components. This is accomplished by applying the reference-guided phase retrieval (RPR) method which has been developed in this work. The MAD phases contain all information about the orientation of the sample removing arbitrariness in the reconstruction process shown in figure 3. After two iterations, the sample structure becomes apparent, consolidates over a couple of iterations, and refines in less than 30 iterations. The resolution of MAD imaging is ultimately given by the observation of interference terms in the speckle patterns at high momentum transfer. In the presented case the resolution of 25nm is limited by statistics.
Lensless MAD imaging can be viewed as an in-line x-ray holography technique which eliminates the need for fabricating small reference structures as in x-ray Fourier Transform Holography. In combination with the RPR algorithm the method is capable of providing unique and rapid reconstructions of a variety of inhomogeneous systems, representing regions with different atomic constituents, chemical composition such as organic functional groups, and magnetic behavior such as changes in moments and their orientations.
A. Scherz, D. Zhu, R. Rick, W. F. Schlotter, S. Roy, J. Lüning, J. Stöhr, "Nanoscale Imaging with Resonant Coherent X Rays: Extension of Multiple-Wavelength Anomalous Diffraction to Nonperiodic Structures", Phys. Rev. Lett. 101, 076101 (2008).