Stanford Synchrotron Radiation Lightsource

Figure 1. New 13 Tesla magnet facility for x-ray scattering and EXAFS on SSRL beam line BL7-2.

Many condensed matter systems can be described as large collections of microscopic entities, each of which can be in one of two possible states. For example, in many anisotropic magnets spins can point in one of two directions along a unique crystalline axis.  In a liquid-gas phase transition, molecules will be in either the gas or liquid phase.  When the microscopic entities interact, they may exhibit collective long-range order.  A collection of two-state particles with near-neigh bor interactions is known as an Ising system.  This simple system is very important because the behavior that an Ising system displays as it undergoes a transition to long-range order has universal features that are independent of the details of the two-state particles or their interaction.  The Ising model is one of the simplest and most ubiquitous models for spontaneous long-range order and, hence, is perhaps the most important model in statistical physics, with many applications that go well beyond the realm of physics.

For the pure three-dimensional (d = 3) Ising model, there is extremely good agreement among theory, simulations, and experiments [1]. Hence, the model can be considered well understood. Through the years, the intellectual value of the Ising model has grown, particularly as a model of disorder. One of the most important of these models of disorder occurs when a random field is imposed which couples directly to the order parameter of th e system, the Random Field Ising Model (RFIM). The most studied realization of this random-field Ising model (RFIM) is the diluted antiferromagnet in an applied magnetic field. An archetypal system is FexZn1-xF2. In this model, the magnetic moments are disordered above a magnetic field dependent critical temperature, Tc(H). When the temperature drops below Tc(H), the high symmetry of the disordered system is broken and the magnetic moments order. The amount of order in the symmetry-broken system is reflected by the order parameter, chosen such that it is non-zero when the symmetry is broken in ordered state and equal to zero in the symmetric disordered state. Unlike the pure d = 3 Ising model, there is, so far, poor agreement between theory and simulations on the one hand and experiments on the other [1]. In the experimental RFIM, as in all antiferromagnets, the order parameter is the staggered magnetization  

M_s = M₀t^β (1)

where, t = ( T_c(H) - T ) / T_c(H) is the reduced temperature. For the RFIM, this order parameter has previously been poorly characterized. A recent study [2], which makes use of the new high-field magnet facility on Beam Line 7-2 at SSRL, is the first characterization of the exponent β.  The result by Ye and co-workers, β = 0.16 +/- 0.02, provides an important quantitative experimental contribution toward a comprehensive understanding of the RFIM.  Interestingly, it is in stark disagreement with simulations, which predict the value of b to be very close to zero.

Measurements of b have proven very difficult in practice.  First, neutron scattering on these hig h-quality crystals suffers greatly from the effects of extinction and techniques for x-ray scattering in a high magnetic field, which are extinction-free, had to be developed [3]. Second, for magnetic concentrations xbelow the vacancy percolation threshold [4], xv = 0.754, microscopic domain formation obscures the RFIM critical behavior below the transition at T_c(H) in Fe_xZn_1-xF₂. Onl y recently has it been realized that microscopic domains do not form for x > 0.76. Such high magnetic concentrations require high magnetic fields for studies of critical behavior, and the high-field magnet shown in Fig. 1 enabled such experiments at SSRL, as reported recently in Physical Review Letters [2].

A focused monochromatic x-ray beam was obtained from the wiggler spectrum via a Si(111) double-crystal monochromator. X-ray energies between 13.5 and 14 keV were u sed, which resulted in a penetration depth of about 60 mm. The energy was tuned to minimize energy-sensitive multiple scattering [3]. The temperature of the crystal, mounted in a He atmosphere, was stable to approximately 10 mK.

Conventional thermal-cycling procedures were employed to take data. In the zero-field-cooled thermal cycle (ZFC) the sample is cooled in zero field below T_c(H), the field is applied, and the sample is warmed throughTc(H), waiting at each temperature at least 20 min before taking data to let the system equilibrate.  In the field-cooled procedure (FC) the sample is cooled through T_c(H) in the field, taking data as in ZFC.  The scattering intensities were measured at the (100) antiferromagnetic Bragg point. The critical scattering contribution was fit using neutro n scattering line shapes[5,6], and subtracted before determining the order parameter exponent.

The x-ray Bragg scattering shows hysteresis. The ZFC intensities are higher than the FC intensities. This difference depends slightly on the cooling rate used in obtaining the FC data. The ZFC data are rate independent. Hence, the ZFC data likely represent the correct order parameter measurement. Various measurements near the transition at this concentration have yielded cr itical behavior indicative of a second-order phase transition. Therefore, this appears to be a second-order transition, although an extraordinary one.

After subtraction of the background and the critical scattering, the measured Bragg intensity is proportional to the square of the staggered magnetization:

I_B ~ Ms² (2)

Figure 2.   The ZFC Bragg scattering data for H = 0, 10, and 11 T, corrected for the critical scattering contribution, plotted as the logarithm of the intensity versus the logarithm of t. The solid green and red lines, for H = 10 and 11T, respectively, indicate RFIM behavior with b = 0.16, while the blue line for H = 0 reflects conventional random-exchange behavior with b = 0.35.

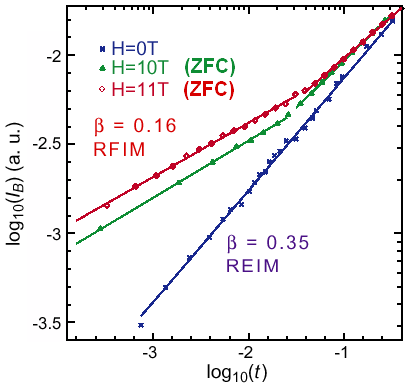
Figure 2 shows a plot of the logarithm of I_B versus the logarithm of the reduc ed temperature at three different fields: 0, 10, and 11 T. The values of T_c(H) were determined from fits to the data. For 0.0007 < t < 0.03 and H = 0, Ye and co-workers find b = 0.35 ± 0.02 (blue line), which agrees well with several experimental and theoretical determinations for the random-exchange Ising model [1]. ForH = 10 an d 11 T, a crossover from random-exchange to RFIM critical behavior occurs near t = 0.03, and the data can be fit to a single power law only in the range 0.0001 < t < 0.03. The fits over this range yield the exponent β= 0.16 ± 0.02 for the combined H = 10 and 11 T data and are in dicated by the parallel green and red lines in Fig. 2.

There does not exist a set of theoretical results that are consistent with all the experiments to date [1]. In particular, Monte Carlo [7] and exact ground state calculations [8,9,10] yield values of b close to zero. Since consistency among numerical and experimental exponents continues to elude us, a comprehensive understanding of the d = 3 RFIM is y et to be achieved. The determination of the order parameter exponent presented here is an important quantitative contribution in this direction.